Aus der FUNKSCHAU 1978, Heft 18
von Ing. (grad.) Werner Eimer und Prof. Dr.-Ing. Hans-Jürgen Vogt in 1978 - überarbeitet und ergänzt von Gert Redlich im April 2012
Phasenkompensierte aktive (zweiwege) Frequenzweiche
In Lautsprecherboxen oder Nf-Verstärkern eingesetzte Frequenzweichen korrigieren den Amplitudenfrequenzgang und verursachen dabei in der Regel erhebliche Phasenverzerrungen.
Der nachfolgende Aufsatz zeigt am Beispiel einer Zweiwege-Frequenzweiche einen Weg zur Lösung des Problems.
Anmerkung : Dieser Fach-Artikel ist recht technisch geschrieben und ich als Redakteur habe ein paar Sachen einfach weggelassen bzw. mit Worten interpretiert. Heute rechnet man das ganze Netzwerk nicht mehr mit dem Rechenschieber oder dem Taschenrechner wie noch vor 30 Jahren. In den anderen Artikeln links im Menu sehen Sie, wie ich die einzelnen Filter der diversen aktiven Boxen (von denen uns der Schaltplan vorlag) selbst "nachgebaut" (also simuliert) habe und im Simulator die Frequenzkurven mit 1 (einem) Klick errechnen lasse.
.
- Bild 1. Übergangsfunktion, Amplitudenfrequenzgang A(co) und Phasenfrequenzgang b(co) I eines linearen Ubertragungssystems
Phasenverzerrungen beeinflussen nachhaltig das Übertragungsverhalten bei impulsförmigen Eingangssignalen, so daß der zeitabhängige Verlauf des Ausgangssignals den des Eingangssignals nicht richtig wiedergibt. Zur Verbesserung der Impulsübertragung einer aktiven Frequenzweiche bzw. eines aktiven Filters soll der Zusammenhang zwischen dem Frequenzgang und der Sprung- bzw. Impuls-Antwort eines Netzwerkes betrachtet werden.
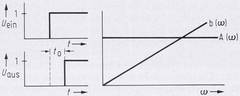
Ein ideales, lineares, verzerrungsfreies Übertragungssystem gibt nach Ablauf der Laufzeit oder Totzeit t0 einen Einheitssprung am Eingang ohne Uberschwingungen unverzerrt am Ausgang wieder. Seine normierte Sprungantwort erhält den Wert 1; sein Amplitudenfrequenzgang A (od) und sein Phasenfrequenzgang b (oo) sind aus Bild 1 zu ersehen.
Wird dieser Gedanke sinngemäß auf eine aus Einzelfiltern bestehende Frequenzweiche übertragen, so muß gefordert werden, daß die Summe der Sprungantworten der einzelnen Filter der Frequenzweiche den Wert 1 hat, um ein fehlerfreies Impulsübertragungsverhalten zu gewährleisten. Ist diese Bedingung erfüllt, so werden alle in einem Signal vorhandenen Teilschwingungen in richtiger Amplitude und Phase wiedergegeben. Diese Zusammenhänge werden im nachstehenden Beispiel näher erläutert.
Anmerkung : Wenn das Eingangssignal (bei uns die Musik) in beide Frequenzweichen eingespeist wird, kommt es im Überlappungsbereich über zwei Lautsprecher wieder raus. Diese beiden Lautsprecher sollten bzw. dürfen das Signal möglichst nicht phasenverschoben angeliefert bekommen, sonst ergäbe das deutlich andere Pegel, im schlimmsten Fall sogar Auslöschungen. In diesem Überlappungsbereich sollten sich im Idealfall die beiden Signale zum Gesamtpegel addieren. Das funktioniert aber nur, wenn im Filter und im Verstärker nichts an der Phase "gedreht" wurde.
.
Vorgabe:
- Bild 2. Netzwerk zur Phasenkorrektur der Frequenzweiche
- Bild 3. Aktiver Tiefpaß 2. Ordnung
- Bild 4. Aktiver Hochpaß 2. Ordnung
Eine aus einem Tief-und Hochpaß 2. Ordnung (12 dB/Oktave) bestehende aktive Frequenzweiche soll auf ideales Impulsverhalten optimiert werden.
Für die Normierung gibt es mathematische Formeln, die ich Ihnen aber ersparen möchte. Und mit Hilfe der Laplace-Transformation kann ich die Sprungantworten errechnen. Im Idelafalle sollte solch eine Gleichung den Wert 1 ergeben, (haben die schlauen Leute herausgefunden). Warum und wieso wäre hier zu technisch.
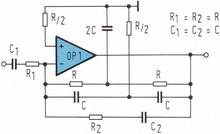
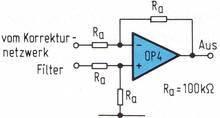
Damit die Gesamtantwort den Wert 1 erhält, muß ein Korrekturnetzwerk gefunden werden, das eine ganz bestimmte Sprungantwort besitzt. Die Rücktransformation würde dann die normierte Übertragungsfunktion (2) des Korrekturnetzwerkes ergeben. Unter der Voraussetzung idealer Verstärkereigenschaften wird die Ubertragungsfunktion (2) durch das Korrekturnetzwerk in Bild 2 richtig wiedergegeben.
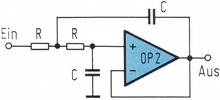
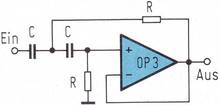
Es handelt sich bei diesem Netzwerk um einen aus einem Tiefpaß (R2, C2) und einem Hochpaß (R1 C1) zusammengesetzten Bandpaß, in dessen Gegenkopplung ein Doppel-T-Filter angeordnet ist. Für den Aufbau von Hoch- und Tiefpaß wurden ebenfalls aktive Schaltungen mit einem Operationsverstärker verwendet (Bild 3, Bild 4).
- Bild 5. Subtrahierer zur Zusammenschaltung von Hochoder Tiefpaß mit dem Korrekturnetzwerk
Die Eck- bzw. Resonanzfrequenzen der drei aktiven Schaltungen in Bild 2, 3 und 4 werden auch wieder durch eine Gleichung bestimmt, wobei sich eine sehr einfache Dimensionierung ergibt.
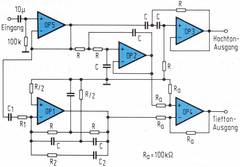
Bei der praktischen Ausführung der korrigierten, aktiven Frequenzweiche wird das Ausgangssignal des Korrekturgliedes dem Signal des Hoch- oder Tiefpasses angefügt. Wegen der Inversion durch den Verstärker OP 1 wird es subtrahiert [Bild 5).
- Bild 6. Gesamtschaltbild einer phasenkompensierten aktiven Frequenzweiche
Und das ist unrealistisch.
Der Nachbau der Frequenzweiche ist relativ einfach. Er erfordert lediglich "einige" Erfahrung im Umgang mit Operationsverstärkern.
- Anmerkung : Das ist nicht nur leicht übertrieben, es ist absolute Profi-Arbeit, die sich die allermeisten Hersteller nicht nur aus Kostengründen gespart hatten. Die Entwickler hatten noch gar nicht das Wissen, das die Diplom-Physiker und Diplom-Ingenieure in langen Jahren mühsam gelernt hatten.
.
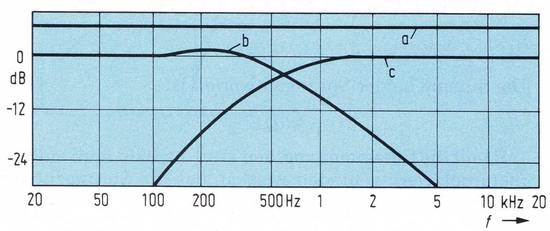
Die aus Bild 6 ersichtliche Schaltung wurde aufgebaut und praktisch erprobt. Hierbei wurde das Korrekturglied dem Tiefpaß zugeordnet. Bild 7 zeigt die einzeln gemessenen Frequenzgänge.
- Bild 7. Amplitudenfrequenzgang der Frequenz-Weiche; a = Gesamt-Frequenzgang, b = Tiefton-Ausgang, c = Hochton-Ausgang
Die Kurve a stellt den addierten Gesamtfrequenzgang der Frequenzweiche dar, die Kurve b gibt den Amplitudengang des Tiefpasses und des Korrekturgliedes an, Kurve c die Charakteristik des Hochpasses. Bemerkenswert ist, daß sich die Flankensteilheit des Tiefpasses durch das Korrekturglied von 12 dB/Oktave auf etwa 6 dB/Oktave vermindert.
Dies ist ein gewisser Nachteil, es muß also ein Baßlautsprecher Verwendung finden, der auch den aus Bild 7 ersichtlichen Frequenzbereich abstrahlt. Weiter verschiebt sich die resultierende Übergangsfrequenz (Schnittpunkt der Kurven b und c) um den Faktor 2. Wird das Korrekturglied dem Hochpaß zugeordnet, so verschiebt sich die Übergangsfrequenz um den Faktor 0,5. Dies muß bei der Dimensionierung berücksichtigt werden.
Die meßtechnische Überprüfung ergab, daß die theoretischen Überlegungen in vollem Umfang bestätigt werden. Die Addition von Hoch- und Tiefpaß sowie des Korrekturnetzwerkes weist im gesamten Übertragungsbereich keinen Phasenfehler auf. Es sei angemerkt, daß sich nach diesem Prinzip auch 3- oder 4-Weg-Frequenzweichen konstruieren ließen. Auch ist es möglich, Filter höherer Ordnung zu kompensieren, nur ergeben sich dabei wesentlich kompliziertere Korrekturschaltungen.
Kommentar :
Bereits in 1980 hatte man Lautsprecher Chassis verfügbar, die in ganz bestimmten engen Frequenzbereichen sehr gut waren, darüber und darunter aber bescheiden waren. Darum wurden in hochwertigen aktiven Boxen aktive Frequenzweichen mit mindestens 12 dB/Oktave Flankensteilheit gefordert. 6 dB/Oktave reichte da überhaupt nicht aus.
Eigentlich hätte die Flankensteilheit der Filter bei 18 dB/Oktave liegen sollen, damit die Überlappungen der Frequenzbereiche im Bereich der Übergangsfrequenzen so gering wie möglich wäre.
Darum ist die obige Überlegung der idealen Phase eines Filters mit dem Verlust an Steilheit des Filters gegenüber den Verschlimmbesserungen einer Phasendrehung abzuwägen - gegenüber einem vielleicht noch aufwendigeren aber steileren Filter.
In allen bei uns befindlichen 4 (inzwischen 5) aktiven Lautsprecherboxen (-paaren) aus den Jahren 1973 bis 1982 wurde von dem oben dargelegten Wissen kein Gebrauch gemacht. Vermutung: Der Aufwand war einfach zu hoch, das Ergebnis am Ende unbefriedigend.
Bei den passiven Frequenzweichen sind solche Kompensations-Tricks sowieso überhaupt nicht möglich, weil sonst enorme Pegelverluste eintreten.
.
