Das hier ist Teil 2 von
"Das System Schallplatte"
Wenn Sie beim Suchen hier gelandet sind, gehen Sie bitte eine Seite zurück und beginnen Sie auf der einführenden Seite hier.
.
Die Physik des "mechanischen schwingenden Systems"
Warum ich immer wieder den Begriff des mechanischen !!! "schwingenden Systems" benutze, hat folgenden Grund :
Ein mechanisches schwingendes System hat immer eine Masse und die ist immer größer als "Nichts" !!!.
Selbst wenn sich diese Masse im Milli- oder Mikrogramm- Bereich bewegt, ist die Masse größer als "0". Das ist extrem wichtig, denn man kann das "Geschehen" auf einem Blatt Papier (oder an der Wandtafel) ausrechnen (quasi in einer oder mehreren mathematischen Formeln darstellen).
Mehr über die Mathematik steht hier samt der zugehörigen Formeln. Und wenn in solch einer komplexen mathematischen Formel der Wert der Masse einfließt, ist es sehr wichtig, ob der Wert gleich "Null" ist oder größer als "Null" ist.
Der Mathematiker erlaubt z.B. prinzpiell keine Division durch "Null" und auch nur ganz selten Multiplikationen mit "0". Das Ergebnis wäre zum Beispiel entweder völliger Unsinn oder es würde unendlich groß werden oder diese Formel ergibt überhaupt kein Resultat und damit keinen Sinn.
Anmerkung aus der TH Darmstadt. Unser Mathe-Profesor gab uns damals Aufgaben, mit denen wir uns viele Tage den Kopf zermarterten, um dann Tage später zu hören, für diese Gleichung oder Formel gibt es keine Lösung, die sei unlösbar. Das war eine fatale Motivation für uns Jungingenieure.
.
Ein Beispiel bezüglich der Erkenntnisse aus der Mathematik
Professor Dr. Hausdörfer, Leiter der Produkt-Vorent-wicklung und Digitaltechnik der ehemals sehr renommierten Robert Bosch Fernseh GmbH in Darmstadt schuf sich 1964 gleich zu Beginn seiner Mitarbeit in der neuen Firma "keine Freunde" (man könnte das auch anders herum formulieren), als er behauptete, die (Halbleiter-) Funktion des Orthicons und auch des Super-Orthicons könne man mathematisch in einer Formel darstellen.
Der junge Doktor, der gerade erst 2 Jahre vorher seine Physik-Promotion in Halbleitertechnik an der UNI Aachen abgeschlossen hatte, stieß bei den beiden (ur)alten Chefs mit deren empirischem (analogen) Vorkriegeswissen auf heftigsten Widerstand.
Das Problem war aber so simpel und einfach, daß "man" sich Jahre später (aber ohne Gesichtsverlust natürlich) in aller Form (auf dem Hausflur) entschuldigte. Diese analoge Fernsehaufnahmeröhre namens Super-Orthicon krankte an der mangelnden Lichtempfindlichkeit im Bereich "rot". Die Bühnen- bzw. Szenenbeleuchtung mußte extrem hell sein, damit die 3-Röhren- Kamera ein einigermaßen rauschfreies Studio-Farbbild ablieferte. Die alten Herren entwickelten die vordergründig geniale Idee des sogenanten "Elektronen-Vervielfachers" mit 6 Vervielfacher-Stufen. Und Dr. Hausdörfer rechnete noch während der Entwicklung vor, daß selbstverständlich das zu bekämpfende Grundrauschen der Elektronen natürlich auch mit vervielfacht werden würde, was aber heftigst abgestritten wurde.
Leider war es aber so, das Rot-Signal war jetzt zwar deutlich stärker - aber mit genau dem gleichen sichtbaren Rauschanteil wie vorher. Und so begann unser bundesdeutsches Farbfernsehen - es war damals 1967 richtig peinlich - mit holländischen Philips LDK3 Farbkameras, weil den alten Herren (es waren alles Doktoren) erst sehr spät die Einsicht kam.
.
Bereits die Theorie sagt : Ein schwingendes System kann sich nur auf Kurven bewegen . . .
und Kurven kennen keine Ecken (per Definition). Ich könnte also mit dem Schneidstichel theoretisch eine perfekt rechteckig geformte Rille oder eine theoretisch perfekt geformte Dreiecks-Rille schneiden.
Doch das trügt. Auch der Schneid-Stichel kann seine Bewegungs- richtung nicht abrupt ändern. Und die Platte dreht sich ja bereits. Also Rechteck-Modulationen gibt es so nicht, es wären im theoretisch günstigsten Falle Rauten.
Auch bei einer elektrisch angesteuerten Dreiecksform ist die erzwungene Umsteuerung der Bewegungsrichtung des Stichels nur theoretisch eine scharfkantige "Ecke". Oberflächlich sieht die Rille vielleicht wie eine perfekte Zick-Zack Rille aus, doch unter dem Mikroskop sieht man bestimmt, daß die "Ecken" am Ende doch rund sind. (Bilder kommen noch)
.
Der begriffliche Unsinn mit den "Rechteck-Schwingungen"
Hier reflektiere ich auf hunderte von Abtaster-"Tests", die ich gefunden habe und die mit (dargestellten fotographischen) Rechtecksignalen protzen, es aber nicht (oder höchst selten) erklären, wie diese abfotografierten Rechtecksignale erzeugt werden bzw. wie man sie darstellt.
Also grundsätzlich kann man auf Schallplatten keine rechteckförmige Rille abtasten. Das geht mechanisch nicht. Weiterhin könnte ein magnetischer Abtaster solche Rillen-Signale auch gar nicht korrekt in adequate oder funktionsgleiche elektrische Signale umwandlen, denn der magnetische Abtaster erzeugt immer nur dann eine Spannung (z.B. ein Audio-Signal), wenn das schwingende System bewegt wird (es gibt da nur eine Ausnahme = das Piezo-/Kristallsystem).
.
Es gibt aber einen Trick speziell für diese magnetischen Abtaster. Der Ingenieur schneidet ein (theoretisch) dreieckförmiges Signal auf die Platte, wohl wissend, daß auch hier die mechanische Abtastung enorme Probleme bereitet.
Bereits die geschnittene Rille ist nicht absolut "dreieckförmig", sondern nur hinreichend "eckig". Denn die Ecken sind alle leicht oder ganz wenig abgerundet.
.
Wofür brauche ich eigentlich ein Rechtecksignal ?
Zuerst nochmal zurück zum Rechteck : Mit einem elektronischen Signalgenerator kann ich "natürlich" ein rechteckförmiges ideales eckiges Signal erzeugen, weil ich hier absolut keine Masse bewegen muß. Dieses Signal kann ich in einen Verstärker einspeisen und dort das Ausgangssignal betrachten. Auch wenn das eingespeiste Signal auf dem Oszilloscope optisch perfekt rechteckig aussieht, wird aus dem Verstärker fast immer ein abgewandeltes bzw. verändertes Signal herauskommen.
An der jeweiligen Veränderung ersehe ich, wie gut der Verstärker die ganz hohen und die ganz niedrigen Frequenzen verstärken kann. Wie das im Einzelnen geht und warum, steht an anderer Stelle - bei den Verstärkern.
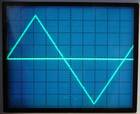
Kritisch ist nämlich der Richtungswechsel der Signalspannung des Rechtecksignales, also wenn die Signal-Flanke abrupt von der Nullinie nach oben oder nach unten springt (siehe Bild rechts).
Dann muß die Elektronik einen sehr hohen Frequenzbereich verstärken können, weil es sehr schnell (theoretisch unendlich schnell) gehen muß. Kann der Verstärker diese hohen Frequenzen aber nicht mit gleichem Pegel verstärken, werden die "Dächer" schräg und die ehemals perfekten "Ecken" gerundet bzw. rundlich.
Diese zuerst einmal recht grobe optische Erkennung der höchsten abzutastenden Frequenzen möchte man auch bei den Schallplatten benutzen. Doch erstens kann eine Nadel nicht frontal gegen eine Rillenwand knallen und zweitens wird während des Dachs des theoretischen Rechtecksignales (siehe Bild) keine Spannung bzw. kein Strom erzeugt. Das dann auf dem Oszilloscope angezeigte Bild würde die Bewegung der Nadel bzw. dieses Signal überhaupt nicht mehr sinnvoll nachbilden bzw. abbilden.
.
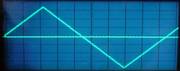
Die Dreiecks-Modulation schneiden und dann abtasten
Wegen der mechanischen Probleme bei der unmöglichen Abtastung eines Rechtecks weicht man auf ein hinreichend optimales Dreiecks-Signal aus. Der Schneidstichel bekommt ein perfektes Dreiecksignal zugeführt und müsste jetzt eine perfekte dreieckige Rille schneiden (können).
Doch aufgrund der oben beschriebenen Masse des Stichels kann er das nicht. Es ergibt auch nur eine sogenannte "hinreichend" genaue Dreieckmodulation. Für eine perfekte Dreieckrille müsste der Stichel - und sei er noch so leicht - mit einer "unendlich großen" Kraft angetrieben werden. Denn die Masse ist eben nicht "0" - wie beim elektronischen Signalgenerator.
.
Die mathematische Formel für die perfekte Laufrichtungsumkehr selbst einer Dreieck-Rille (also noch nicht mal einer Rechteck-Rille) ist sehr komplex. Diese Formel enthält die Komponenten (Größen) unter anderen der "Masse des Stichels", des "Widerstandes des zu schneidenden Kunststoff-Materials" und der aktuellen Bewegungsfrequenz. Ist die Masse des Stichels nicht "absolut" Null (und das kann sie nie werden), so muß die verfügbare Kraft des Antriebes "absolut" unendlich groß sein, sonst funktioniert schon die (mathematische) Theorie nicht. Der Stichel müsste damit nämlich unendlich schnell die Bewegungsrichtung umkehren (können).
.
Schon die Meßschallplatte hat ihre physikalischen Grenzen
In der Praxis ist der 2 x 250 Watt Sinus Verstärker der Neumann VMS 80 Schneide- maschine eben nur 2 x 250 Watt stark - und eben nicht 2 x 100.000 Watt oder noch mehr.
.
Und bei der Wiedergabe kann der Abtastdiamant die Bewegungsrichtung auch nicht abrupt, also unendlich schnell ändern. Er müsste auch fast rechtwinklig um die Ecke rasen. Aber zum Glück ist die "Ecke" einer solchen Dreiecks-Rille sowieso leicht rund und zweitens erfolgt die Richtungsänderung in Richtung der abgeschrägten Flanke.
.
Um also eine solche Meßschallplatte mal auf die überhaupt machbare Qualität hin zu untersuchen, wäre natürlich der Laser-Plattenspieler ideal. Solche Laser-Abtaster gibt es bereits, die kosten aber eine richtige Stange Geld. Alleine damit kann man die beiden Rillenflanken absolut trägheitslos (ideal) abtasten und somit alle Schwächen und Probleme, die mit der - auch noch so kleinen - Masse der Diamantnadel verbunden sind, umgehen.
.
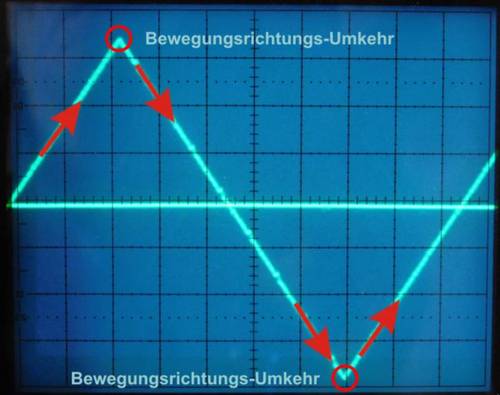
Die Grenzen des Abtasters
Betrachten wir diese Dreieckrille mal etwas genauer. Bei niedrigen Frequenzen des Dreiecksignals (unterhalb von 1kHz) ist der "Winkel im Knick" - also an dem Punkt der Bewegungsrichtungsumkehr - noch moderat - irgendwo zwischen 160" bis 175°. Mit jeder weiteren Steigerung der Frequenz wird der "Knickwinkel" schärfer und irgendwann hat er die 90° Marke erreicht, bei der der Abtastdiamant quasi an die Wand knallen würde. Bei der maximal möglichen Frequenz gibt es daher recht simple verständliche Grenzwerte. Die allermeisten Meßschallplatten mit solchen Dreiecksrillen arbeiten maximal mit einer 1 kHz Frequenz.
Auch ist der "Knickwinkel" von der Rillen-Position des Abtasters (der Position auf dem Radius) abhängig, also auf den äußeren Rillen oder in der Mitte der Platte oder bereits ganz innen kurz vor der Auslaufrille.
Je weiter die Rille nach innen läuft, desto kürzer wird die verfügbare Rillenlänge für diese Dreieckform und damit steigt - bei nachwievor gleicher Amplitude (Auslenkung) der "Knickwinkel" in Richtung der kritischen 90 Grad. Wie weiter oben gesagt, ein richtiger Knick ist es nicht. Dennoch muß die Abtastspitze einiges aushalten.
.
Um mal ein Gefühl für die Kräfte zu bekommen, ein Beispiel :
(1) Sie fahren mit dem Fahrrad auf dem Fahrradweg und ein KFZ biegt abrupt vor Ihnen rechts ab und schneidet Sie ganz leicht. Winkelgröße bzw. Aufprallwinkel wären dabei etwa 10°. Das fangen Sie durch ein deutliches Ausbrechen bzw. Schlenkern aus Ihrer Fahrtrichtung gerade noch ab, vielleicht sogar ohne zu stürzen.
(2) Nehmen wir an, der Autofahrer biegt deutlich schärfer rechts ab, also etwa mit einer Winkelgröße bzw. einem Aufprallwinkel von etwa 30°, dann wirft es sie bereits vom Fahrrad. Sie landen leicht verletzt im Rinnstein
(3) Nehmen wir an, der Autofahrer reißt das Lenkrad brutal rechts rum und schneidet Sie mit einer Winkelgröße bzw. einem Aufprallwinkel von etwa 60°, dann knallen sie bereits voll in die Beifahrertür rein und fliegen hochkant über das KFZ rüber, sie können überhaupt nicht mehr ausweichen.
(4) Nehmen wir zuletzt an, zum Glück rein theoretisch, der Autofahrer mißachtet die "Rechts vor Links Regel" und steht auf einmal direkt vor Ihnen. Dann knallen Sie "rechtwinkelig", also mit einer Winkelgröße bzw. einem Aufprallwinkel von 90° auf das KFZ ohne jede Chance, das irgendwie abzufangen. Sie knallen mit der vollen kinetischen Energie der jeweiligen Geschwindigkeit (umgangssprachlich : mit woller Wucht) auf das Hindernis. Ergebnis: Totalausfall. Die Abtastnadel würde abbrechen bzw. Sie als Radfahrer sind jetzt tot.
.
Sicher hinkt der Vergleich ein wenig . . .
. . . denn der Radfahrer fährt im Vergleich erheblich langsamer als die Abtastanadel in einer mit 18.000 Hz schlingernden Rille. Dafür wiegt ja die Diamantspitze auch erheblich weniger als ein Radfahrer. Aber wie gesagt, man bekommt eine kleine Vorstellung der wirkenden Kräfte.
Jetzt leuchtet es ein, wie steil die Winkel in dieser Dreickrille maximal sein dürfen, damit die Nadel das mechanisch überhaupt aushält. Weiterhin darf natürlich auch die Rille an sich nicht abrasiert werden bzw. ausgeschlagen werden.
.
Merkwürdig, es sind keine SHURE Testplatten aufzutreiben
Ich möchte jetzt die Rillen mit diesen Dreiecksformen fotografieren. Auf einmal hat niemand diese SHURE TR101 und TR111 und TR114 Platten mehr, selbst die mir bekannten Experten suchen vergeblich.
.
Es gibt noch mehr Informationen über die Rechtecksignale
.