Um Mißverständnissen vorzubeugen, hier eine detallierte Ausführung über die Technik der Kondensatoren aus 1975
Der erste Einführungs-Artikel über Kondensatoren war bewußt einfach bzw. vereinfachend dargestellt. Da das Thema aber weitaus komplizierter ist, hier ein wirklich fundierter Artikel für angehende Techniker oder Leser, die bereits ein paar Vorkenntnisse haben.
Die Texte und Bilder stammen zum Teil aus einem sehr guten Philips Lehrbrief aus 1975. Sicher hat sich in den letzten 30 Jahren das ein oder andere Detail verändert oder ist sogar ganz weggefallen, doch die physikalischen und chemischen Grundlagen sind die Gleichen geblieben.
In unserer Redaktion stehen mehr als 30 Elektronik-Fachbücher aus den letzten 50 Jahren, die alle versuchen, das physikalische Grundlagen-Wissen irgendwie zu vermitteln. Nur wenige haben eine so verständliche Ausdrucksweise wie die Philips Lehrbriefe. Dennoch mixen wir die jeweils besonders guten Kapitel, Passagen oder Absätze aus mehrern Publikationen zusammen.
.
Die Kapitel 1.0 bis 3.1 umfassen ganz allgemeine elektrotechnische Grundlagen und werden für das Verständnis dieses Artikels vorausgesetzt.
.
3.2. Kondensatoren allgemein
Kondensatoren bestehen im Prinzip aus zwei Metall platten oder -folien, die sich in einem bestimmten Abstand gegenüber stehen. Diese sogenannten Beläge berühren sich nicht und sind durch einen Isolator voneinander getrennt. Im einfachsten Fall ist dies Luft, es lassen sich auch Glimmer. Glas oder verschiedene Kunststoffe und keramische Materialien verwenden. Die Elektronen in den Metallplatten können neu also nicht durch den Isolator von einer Platte zur anderen gelangen.
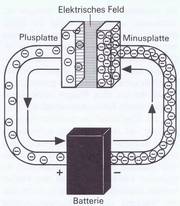
In einem Beispiel soll dies näher erklärt werden. Um es besonders deutlich zu machen, wurden die in den Bildern 3.12—3.15 angedeuteten Kondensatorplatten nicht parallel zueinander, sondern voneinander wegweisend angeordnet, damit ein möglichst großer Isolationsabstand vorhanden ist. In der Verbindungsstelle der beiden Platten sind eine Spannungsquelle (Batterie), ein Strommesser (Drehspulamperemeter) und ein ganz normaler Schalter eingebaut.
Wie funktioniert ein Kondensator - ein Beispiel
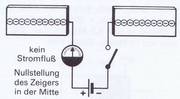
Wie wir wissen, können sich in einem offenen Stromkreis normalerweise keine Elektronen bewegen, d. h. es fließt kein Strom. Dieser Zustand ist in Bild 3.12 zu sehen, worin außerdem noch der Schalter geöffnet ist. Die schematisch angedeuteten Elektronen sind auf beiden Platten gleichmäßig verteilt. Das Instrument (mit Nullpunkt in der Mitte) zeigt keinen Stromfluß an.
Dies ändert sich jedoch beim Schließen des Schalters. Ein empfindliches Instrument würde im Augenblick des Einschaltens der Spannung einen kurzen, schwachen Stromstoß anzeigen.
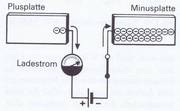
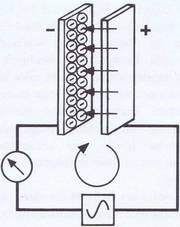
In Bild 3.13 ist dieser Moment angedeutet: der Zeiger schlägt nach rechts aus. Es muß also eine Elektronenbewegung in dem offenen Stromkreis stattgefunden haben! In welche Richtung sich die Elektronen bewegten, geht ebenfalls aus Bild 3.13 hervor: wir sehen eine Ansammlung auf der Platte, die mit dem negativen Spannungspol verbunden ist, während die positive Platte kaum noch Elektronen aufweist. Sie sind in Richtung der Pfeile zur rechten Seite abgewandert. Wie ist das zu erklären?
Die Antwort ist relativ einfach und ergibt sich aus den folgenden, uns schon bekannten Verhaltensweisen der Elektronen: sie sind stets negativ geladen und bewegen sich (fließen) immer von Minus nach Plus, sie stoßen einander ab (üben also eine Kraft aus). Weiterhin sind sie am Minuspol einer Spannungsquelle immer im Überfluß vorhanden, während am Pluspol ein Elektronenmangel herrscht.
Sehen wir uns unter diesen Gesichtspunkten noch einmal Bild 3.13 an. Nach dem Einschalten der Spannung schieben sich zunächst die Elektronen aus dem Minuspol auf die angeschlossene rechte Platte. Dort müssen sie haltmachen, da sie nicht in den freien Raum hinauskönnen. Sie sammeln sich in großen Mengen an. Außerdem saugt der Pluspol der Spannungsquelle negativ geladene Elektronen von der angeschlossenen linken Platte ab. Diese wandern durch die »Elektronenpumpe« und werden von ihrem Minuspol ebenfalls auf die rechte Plane gedrückt.
Auf der mit dem Pluspol verbundenen Platte entsteht Elektronenmangel und folglich ein Überschuß an positiver Ladung. Auf der mit dem Minuspol verbundenen Platte dagegen stauen sich die Elektronen unter Einwirkung der Spannungsquelle und erzeugen somit einen Überschuß an negativer Ladung. Zwischen den Platten unseres Prinzipkondensators ist durch diesen Vorgang ein Spannungsunterschied entstanden. Man kann auch sagen: der Kondensator ist auf eine bestimmte Spannung geladen worden.
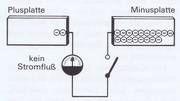
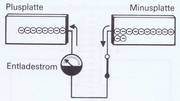
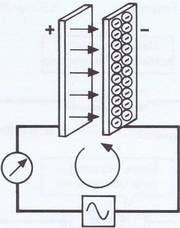
Die elektrische Ladung bleibt auch dann auf den Platten bestehen, wenn die Spannungsquelle bei offenem Schalter abgeklemmt wird (Bild 3.14). Es fließt kein Strom, und der Zeiger des Instruments bleibt auf Null stehen. Schließen wir aber den Schalter, so schlägt der Zeiger zur entgegengesetzten Seite aus (Bild 3.15). Die Elektronen fließen jetzt von Minus (Überschuß) nach Plus, wobei ein Ausgleich stattfindet und der ursprüngliche Zustand wiederhergestellt wird.
3.3. Elektrisches Feld
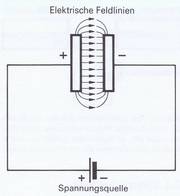
- Bild 3.16 Schema des elektrischen Felds. Die Feldlinien »zeigen« stets zu der am stärksten mit Elektronen besetzten Platte des Kondensators. Man kann auch sagen: Die Feldlinienpfeile geben die Richtung an, in die positive Ladungen gezogen werden. Felder von gleichnamigen elektrischen Ladungen stoßen einander ab, sie »verdrängen« sich gegenseitig.
Was wir in unserer Betrachtung über den Kondensator bisher nicht erwähnt haben, ist eine Erscheinung, die man »elektrisches Feld« nennt. Es tritt überall an den Stellen auf, an denen eine Spannung wirksam wird und ist unsichtbar. Nur an gewissen Anzeichen entdeckt man das Vorhandensein eines elektrischen Felds.
Es zieht beispielsweise Staubteilchen an und macht sich besonders bemerkbar, wenn eine hohe Spannung vorhanden ist. Wir können dies an der Bildröhre eines Fernsehempfängers gut feststellen, weil sich an dem Frontglas der Röhre immer wieder Staub ansammelt. Kein Wunder, denn die Bildröhre arbeitet ja mit einer Hochspannung bis zu rund 20000 Volt! (Gleichspannung)
In Bild 3.16 ist das elektrische Feld zwischen den Platten durch Kraft oder Feldlinien angedeutet. Die elektrischen Feldlinien treten auf der an Plus liegenden Platte in den freien Raum aus und werden von der an Minus liegenden Platte aufgenommen. Leider können wir die Feldlinien nicht in einem einfachen Versuch sichtbar machen und müssen uns mit der zeichnerischen Darstellung zufriedengeben.
Wenn man die in Bild 3.12—3.15 angedeuteten Platten einander mit geringem Zwischenraum gegenüberstellt, erhält man das einfachste Beispiel für einen Kondensator. Es deckt sich dann mit Bild 3.16 und wurde im Bild 3.17 in einer vereinfachten Form dargestellt, um die Elektronenbewegung noch einmal zu verdeutlichen.
Wir stellen wiederum fest, daß die Elektronen vom Pluspol angezogen und vom Minuspol auf die negative Plattenseite gedrückt werden. Sie wirken so als elektrisches Feld auf die gegenüberliegende Platte ein (gestrichelt dargestellt). Zusätzlich zur Wirkung des Pluspols werden dadurch die Elektronen von der positiven Plattenseite fortgeschoben. Je höher die angelegte Spannung und je kleiner der Plattenabstand ist, um so kräftiger wirkt sich diese »Elektronenverschiebung« aus.
Der dabei auftretende kurzzeitige, einmalige Stromfluß zu und von den Platten wird als Ladestrom des Kondensators bezeichnet (s. auch Bild 3.13). Wenn wir beide Platten mit einem Widerstand oder einem Draht verbinden, wird sich der bestehende Spannungsunterschied ausgleichen. Die Elektronen fließen dabei vom Überschuß- in das Mangelgebiet (s. auch Bild 3.15). Den entstehenden Stromfluß nennt man Entladestrom.
Nach dem Ausgleich des Elektronenunterschieds ist natürlich keine Spannung mehr im Kondensator vorhanden und das elektrische Feld ist ebenfalls verschwunden. Es baut sich erst dann wieder auf, wenn erneut eine Spannung an die Kondensatorplatten angeschlossen wird.
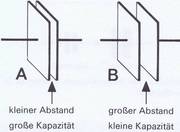
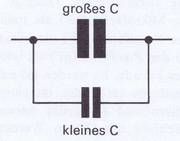
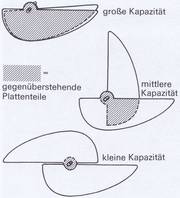
Ein Kondensator kann also mit einer Gleichspannung geladen werden und somit Elektronen bzw. Elektrizität speichern. Sein Fassungsvermögen hängt von der Größe der Platten oder Metallfolien ab und wird Kapazität genannt (Bild 3.18). Der Kapazitätswert ist ferner vom Plattenabstand abhängig: großer Abstand — kleine Kapazität (Bild 3.19). Eine Rolle spielt auch die Isolation zwischen den Platten: Ihre Wirkung ist z. B. bei Luft anders als bei Glas, Papier oder Porzellan. Die isolierende Zwischenschicht nennt der Techniker »Dielektrikum« (sprich: Di-elektrikum).
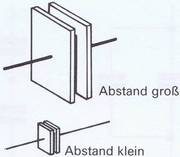
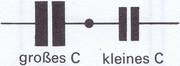
Der Kapazitätswert ist bei gleicher Plattengröße und gleichem Plattenabstand ein anderer, wenn einmal Luft die isolierende Zwischenschicht ist und ein andermal Papier, Pertinax oder ein keramischer Werkstoff. Keramische Werkstoffe eignen sich sehr gut als Dielektrikum, u.a. weil sie vortrefflich isolieren und den Kondensator relativ unabhängig von äußeren Einflüssen (z. B. Feuchtigkeit) machen. Die Isolation verhindert ein Durchschlagen der Spannung vom einen Belag des Kondensators auf den anderen. Das hat natürlich gewisse Grenzen, und für höhere Spannungen muß man daher die Isolation verstärken. So kommt es. daß ein äußerlich großer Kondensator den gleichen Kapazitätswert haben kann wie ein viel kleinerer (Bild 3.20).
Das allgemeine Schaltzeichen
Das allgemeine Schaltzeichen für den Kondensator ist in Bild 3.21 angegeben. Als Maßeinheit für die Kapazität (Formelzeichen C) verwendet man das Farad, sein Kurzzeichen ist F.
Weil es eine große Einheit ist, hat man wieder eine Unterteilung vorgenommen. Gängige Werte sind das Mikrofarad (uF) als millionster Teil, das Nanofarad (nF) als milliardster Teil und das Pikofarad (pF) als billionster Teil eines Farads. Es werden jedoch auch Kondensatoren verwendet, die einige tausend Mikrofarad Kapazität haben. Um hier gleichfalls mit kleinen Wertangaben arbeiten zu können, benutzt man die Einheit Millifarad (mF).
1F = 1000 mF
1mF = 1000 uF
1uF = 1000 nF
1nF = 1000 pF
Die Bezeichnung Farad ist abgeleitet vom Namen des englischen Physikers Michael Faraday - 1791-1867.
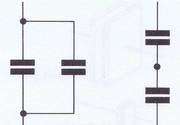
Wenn Kondensatoren zusammengeschaltet werden sollen, so kann das entweder in Parallel oder in Reihenschaltung geschehen (Bild 3.22). Die Gesamt-Kapazität wird in beiden Fällen nach ähnlichen Formeln wie bei Widerständen ermittelt. Bei der Parallelschaltung vergrößert sich der Kapazitätswert, weil eine Summierung der Einzelwerte erfolgt. Die Flächen der Kondensatoren bestimmt die Gesamtkapazität. Durch den größeren Abstand der Platten verringert sich die wirksame Kapazität nochmals. Kondensatorbeläge werden addiert (Bild 3.23a). Größere Fläche = größere Kapazität.
.
3.4. Zeitkonstante
Es wurde bereits vom Lade- und Entladestrom eines Kondensators gesprochen, den man an eine Gleichspannung schaltet. Der Verlauf beider Ströme kann in einem Kurvenbild dargestellt werden, das in Bild 3.25 zu sehen ist. Wenn der Kondensator bei geschlossenem Schalter über einen Widerstand geladen wird, so hängt die Ladezeit vom Wert des Widerstands und des Kondensators ab, nicht aber von der angelegten Spannung.
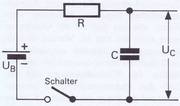
Die Ladeschaltung nach Bild 3.26 enthält die Spannungsquelle UB, den Ladewiderstand R, den Kondensator C und einen Schalter, mit dem der Stromkreis geschlossen wird.
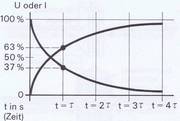
Wird die Spannungsquelle UB angeschlossen, so steigt die Spannung U, nach der in Bild 3.25 angegebenen Kurve an, die man Exponentialkurve nennt. Der Spannungsanstieg erfolgt zunächst recht schnell und nimmt dann einen flacheren Verlauf. Anders sieht es mit dem Ladestrom Ic aus. Wie Bild 3.25 zeigt, springt er mit dem Einschalten auf 100 % seines Werts (der Ladestrom wird vom Widerstand begrenzt), um dann in einer der Spannung entgegengesetzten Kurvenform abzufallen.
An einem Kondensator ist also der Strom stets vor der Spannung wirksam. Für die Ladezeit gibt es eine Formel, aus der man ersehen kann, wann bzw. wieweit der Kondensator geladen ist. Dies wird in sogenannten Zeitkonstanten angegeben. Der griechische Buchstabe in der Formel wird »tau« ausgesprochen.
Einzusetzende Werte sind normalerweise Ohm und Farad, man kann aber zumeist mit Megohm und Mikrofarad praktischer rechnen. Die Zeitkonstante t wird in Sekunden angegeben. Sie sagt aus, daß der Kondensator bei Anschalten einer Gleichspannung nach dem Ablauf einer Zeitkonstante auf 63 % der angelegten Spannung aufgeladen ist.
Nach einer weiteren Zeitkonstante hat sich der Kondensator um weitere 63 % der verbliebenen Restladespannung (37 %) aufgeladen. Nach fünf Zeitkonstanten ist der Kondensator praktisch ganz geladen, denn seine Spannung ist jetzt auf 99% der Ladespannung angestiegen.
Der Ladestrom sinkt im gleichen Verhältnis ab, d. h. nach einer Zeitkonstante beträgt sein Wert z.B. nur noch 37%. Wir können dies aus Bild 3.25 gut entnehmen. Wenn sich der Kondensator über einen Widerstand entlädt, sinkt die Spannung ebenfalls nach der Exponentialkurve ab: das gleiche gilt für den Entladestrom.
3.5. Wechselspannung am Kondensator
Wir haben es bei den bisherigen Erläuterungen immer nur mit Gleichspannungen zu tun gehabt. Ein sehr wichtiges Kapitel ist jedoch auch das Verhalten des Kondensators bei Wechselspannungen und Wechselströmen. Zum besseren Verständnis soll zunächst wieder ein Vergleich mit dem Wasserstrom an die Verhältnisse heranführen.
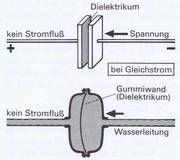
Kondensatoren lassen Gleichstrom nicht hindurch. Ein in einem Gleichstromkreis befindlicher Kondensator unterbindet den Stromfluß, mag sein Kapazitätswert auch noch so groß sein. Schematisch ist dies in Bild 3.27 dargestellt. Befindet sich in einem Wasserstromkreis ein Gefäß mit einer Trennwand aus Gummi, etwa in der Form wie es das Bild zeigt, erhält man damit ein kondensatorähnliches Gebilde. Kommt der Wasserstrom aus einer Richtung (Gleichstrom), dann biegt sich die Gummiwand im ersten Augenblick wohl durch, aber damit hört jeder Bewegungsvorgang auf: das Wasser kann in den Leitungen nicht weiterfließen.
Anders ist es, wenn ein Wasserwechselstrom durch die Leitung geschickt wird. Seine ständige Wechselbewegung bleibt trotz der trennenden Gummiwand erhalten. Sie biegt sich nämlich im Rhytmus der Richtungswechsel des Wasserstroms sowohl nach links als auch nach rechts durch. In der angeschlossenen Leitung bleibt deshalb der Wechselstromfluß erhalten, so als sei kein Hindernis eingebaut (Bild 3.28).
bei Wechselspannung
Wir finden jetzt leichter eine Antwort auf die Frage, was geschieht, wenn statt der Gleichspannung eine Wechselspannung an den Kondensator gelegt wird. Der Unterschied besteht doch darin, daß bei der Wechselspannung eine fortwährende Polaritätsänderung der an den Kondensatorplatten liegenden Spannung stattfindet, während dies bei der Gleichspannung nicht der Fall ist.
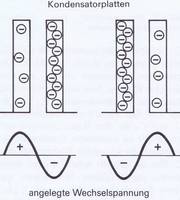
Werden aber die Spannungspole dauernd umgekehrt, so muß auch der Strom dauernd hin und her fließen. Die Wechselspannung läßt deshalb den Elektronenüberschuß abwechselnd auf der linken oder rechten Kondensatorplatte entstehen und polt auch die Richtung des elektrischen Felds entsprechend um. In Bild 3.29 ist dies angedeutet.
Da auch die Ladeströme wegen der Umladungen des Kondensators ihre Richtung immer wechseln und dabei die Elektronen in beiden Anschlußleitungen des Kondensators hin- und herfließen, läßt sich aus diesen Erscheinungen folgender Schluß ziehen: Wechselspannungen und -ströme werden von einem Kondensator (scheinbar) hindurchgelassen, obwohl keine Elektronen durch das Dielektrikum direkt von Platte zu Platte fließen!
Der auftretende Wechselstrom in den Leitungen von und zur Stromquelle beruht auf der Wirkung des wechselnden elektrischen Felds und der dadurch hervorgerufenen wechselnden Elektronenverschiebung auf den Platten des Kondensators. In Bild 3.30 ist dieser Vorgang schematisch dargestellt, man erkennt die wechselseitige Ladung des Kondensators in Abhängigkeit von der Polarität der Wechselspannung.
3.6. Kapazitiver Widerstand
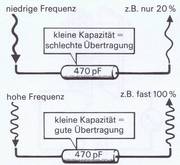
Für die Praxis bedeuten die geschilderten Vorgänge, daß ein Kondensator Wechselspannungen »hindurchläßt«. Es treten dabei Lade- und Entladeströme auf, wie sie zuvor schon bei der Gleichspannung am Kondensator beschrieben wurden. Sie werden bei gleichbleibender Spannung mit steigender Kondensatorkapazität und höher werdender Frequenz größer. Mit anderen Worten: Je größer der Kapazitätswert des Kondensators ist, um so besser wird die Wechselspannung (und der Wechselstrom) übertragen. Auch die Frequenz spielt dabei eine Rolle, denn wie in Bild 3.31 gezeigt, ist bei niedriger Frequenz die Übertragung schlechter als bei hoher Frequenz.
Wenn aber eine Spannung vorhanden ist und ein Strom fließen kann, muß logischerweise auch beim Kondensator ein Widerstand vorhanden sein. Man nennt ihn »kapazitiven Widerstand« oder Wechselstrom- bzw. Blindwiderstand. Er wird mit den Buchstaben Xc bezeichnet und in Ohm angegeben. Seine Größe ist natürlich frequenzabhängig: der kapazitive Widerstand nimmt zu, wenn die Frequenz niedriger bzw. die Kapazität des Kondensators kleiner wird.
Die Formel für den kapazitiven Widerstand lautet:
Hierin ist o (Omega) die sogenannte Kreisfrequenz. Sie begegnete uns auch auf S. 26 bei der Konstruktion einer Sinuswelle. C ist in Farad einzusetzen, damit das Resultat in Ohm angegeben werden kann. Will man die Kondensatorkapazität in uF angeben, muß der Zähler des Bruchs mit 1.000.000 multipliziert werden.
Wir wollen gleich eine Probe machen und den kapazitiven Widerstand eines 10uF Kondensators ausrechnen, der in einem Wechselstromkreis mit der Frequenz von 50 Hz liegt. Es stellt sich folgende Rechnung:
Der kapazitive Widerstand des Kondensators beträgt bei 50 Hz also rund 320 .
Von der Tatsache, daß Wechselstrom durch den Kondensator hindurch übertragen werden kann und der Gleichstromfluß gestoppt wird, macht man in der elektronischen Technik ebenso häufig Gebrauch wie von der Möglichkeit, mit Kondensatoren hoch- und niederfrequente Spannungen zu trennen (sogenannte Filter Wirkung).
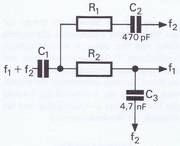
Ein einfaches Beispiel für diese Anwendung zeigt Bild 3.32. Am Eingang der kleinen Schaltung liegen zusammen mit einer Gleichspannung zwei Frequenzen, die getrennt werden sollen.
Der Kondensator C riegelt die Gleichspannung ab und läßt beide Frequenzen durch, weil für sie der kapazitive Widerstand von C vernachlässigbar klein ist. Man teilt dann den Weg durch die Trennwiderstände R1 und R2 auf und fügt danach die Kondensatoren C2 und C3 ein. Ihre Kapazitätswerte stellen für die zu trennenden Frequenzen unterschiedliche kapazitive Widerstände dar. C2 läßt deshalb die hohe Frequenz ungehindert durch (kleiner Widerstand) und sperrt die tiefe (hoher Widerstand). C3 hat durch die Anordnung in der Schaltung eine andere Wirkung. Sein kleiner Widerstand für die hohe Frequenz bedeutet für diese jetzt praktisch einen Kurzschluß gegen Masse: sie wird herausgefiltert und unwirksam gemacht. Für die tiefe Frequenz hat C3 einen hohen Widerstand. so daß diese ungeschwächt weiterfließen kann.
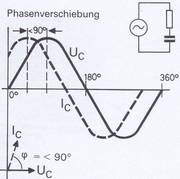
3.7. Phasenverschiebung im Kondensator
Im Abschnitt 2.4. wurde schon grundsätzlich über die Phasenverschiebung zweier Schwingungszüge gesprochen.
Beim Kondensator begegnet uns dieser Begriff wieder. Wir lernten beim Ladevorgang kennen, daß beim Kondensator der Strom zuerst in maximaler Stärke fließt, während die Spannung zum gleichen Zeitpunkt am kleinsten ist.
Im Zuge einer Exponentialkurve nimmt dann die Spannung zu und der Strom ab. Dies gilt im Prinzip auch für Wechselspannungen: nur mit dem Unterschied, daß die Lade- und Entladevorgänge ständig im Rhytmus der wechselnden Polaritäten an den Kondensatorplatten ablaufen.
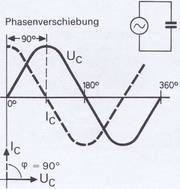
Der Strom im Kondensator eilt also auch bei Wechselspannung der angelegten Spannung voraus, und zwar um 90°.
Es stellt sich demnach eine Phasenverschiebung von einer viertel Periode ein, die in Bild 3.33 gezeichnet ist.
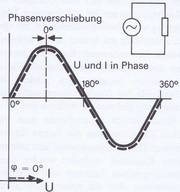
Strom und Spannung erreichen am Kondensator daher nicht zum gleichen Zeitpunkt ihre Maximalwerte. Dies ist nur beim Widerstand der Fall (Bild 3.34).
Schaltet man einen Kondensator mit einem Widerstand in Reihe, dann ergibt sich eine Phasenverschiebung von kleiner als 90°.
In Bild 3.35 ist ein Beispiel gegeben. Wird der Widerstand veränderbar gemacht, erhält man einen sogenannten Phasenschieber, der in elektronischen Schaltungen häufig benutzt wird.
.
3.8. Kondensatoren als Bauelemente
Der Verwendungsbereich von Kondensatoren ist groß. Man findet sie als Elektrizitätsspeicher, zur Glättung von Spannungen und Strömen und zum Abriegeln von Gleichspannungen bei gleichzeitiger Übertragung von Wechselspannungen. Sie spielen zusammen mit Spulen in den Schwingkreisen eine bedeutende Rolle, und sie werden zum Trennen von unterschiedlichen Frequenzen benutzt, zum Ändern des Klangbilds bei Niederfrequenzstufen, zur Entstörung elektrischer Anlagen usw.
Grundsätzlich unterscheidet man zwischen Kondensatoren mit festem Kapazitätswert (Festkondensatoren) und solchen, deren Kapazität verändert werden kann. Hierzu gehören Trimmer und Drehkondensatoren, über die später mehr gesagt wird. Zunächst wollen wir uns mit dem Aufbau der festen Kondensatoren befassen. Wie schon an Bild 3.18 und 3.19 gezeigt, ist die Kapazität eines Kondensators u. a. abhängig von der Größe der sich gegenüberstehenden metallischen Flächen und von ihrem Abstand. Kondensatoren mit hohen Kapazitätswerten würden daher nach dieser Bauweise viel Raum beanspruchen. In der Praxis muß man die Kondensatoren also anders aufbauen.
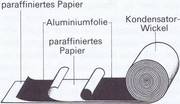
Die Wickelkondensatoren
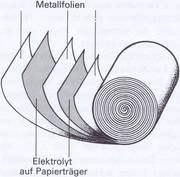
Da gibt es z. B. die Wickelkondensatoren. bei denen zwischen zwei langen Streifen dünner Aluminiumfolic (Beläge) ein isolierender Streifen paraffinierten Papiers oder Kunststoffolie liegt. Ein weiterer Isolationsstreifen kommt unter das Ganze, dann rollt man die Lagen fest zu einem Wickel zusammen. Bild 3.36 zeigt dies schematisch.
Anschließend umpreßt man den Wickel mit Vergußmasse oder umgibt ihn mit einer Kunstharzschicht. Es gibt solche Kondensatoren mit Werten von etwa 100pF bis 1uF. Sie werden u. a. für zahlreiche Aufgaben in Rundfunkempfängern und Fernsehgeräten benötigt. Einige Ausführungen sind in Bild 3.37 gezeigt: sie haben z. B. Betriebsspannungen von rund 25-1000 V.
Gewickelte Kondensatoren haben für Hochfrequenzanwendungen einige Nachteile, die in ihrer Bauweise begründet liegen. Statt ihrer nimmt man deshalb in diesen Fällen Rohrkondensatoren. Das sind röhrchenförmige keramische Kondensatoren mit einem Außen- und einem Innenbelag, die zumeist aus aufgebranntem Silber bestehen. Die Kapazitätswerte dieser Kondensatoren sind daher sehr konstant und liegen zwischen 1 und ca. 50.000 pF. Sie sind mit Lötfahnen oder mit Draht anschlüssen versehen (Bild 3.38).
Scheiben- und Hütchenkondensatoren
Es gibt noch eine Reihe anderer Formen, z. B. Scheiben- und Hütchenkondensatoren. Die gedruckte Schaltungstechnik und insbesondere die ausschließliche Verwendung von Transistoren ließen die Abmessungen der Chassis in modernen Geräten stark schrumpfen. Dem mußten die Bauelemente angepaßt werden. Neben den gezeigten Ausführungen gibt es deshalb heute Kondensatoren, die speziell für Schaltungen mit niedrigen Betriebsspannungen entwickelt wurden. Sie haben sehr kleine Abmessungen, die u. a. durch neue Werkstoffe für die Beläge und das isolierende Dielektrikum sowie verbesserte Fertigungsmethoden möglich wurden.
Um eine Vorstellung von den Größenordnungen zu geben, sind einige neuere Kondensatoren auf Polyester- und Keramikbasis abgebildet. In Bild 3.39 sehen wir oben links einen Standkondensator für gedruckte Schaltungen, der nur 12mm breit ist und der bei einer Betriebsspannung von 250V eine Kapazität bis zu 10nF aufweisen kann. Nicht viel größer sind Scheibenkondensatoren mit Kapazitäten von 47nF und einer Betriebsspannung von 400V. Und bei noch kleineren Spannungen liegen die Abmessungen moderner Kondensatoren mit keramischem Dielektrikum bei nur einigen Millimetern.
Eine Klasse für sich bilden die Elektrolytkondensatoren. Mit ihnen lassen sich hohe Kapazitätswerte bis zu 10.000uF und mehr in einem Becher erreichen. Ihre Abmessungen sind relativ klein. Ein Anschluß kann das Gehäuse sein, ein anderer ragt isoliert heraus. In Bild 3.40 sind die Größenverhältnisse zwischen Hochvolt-Elektrolytkondensatoren und anderen Schaltelementen wiedergegeben.
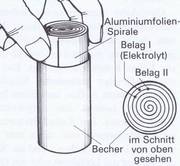
Über die Kapazität
Die Kapazität eines Kondensators ist um so größer, je näher die Beläge einander liegen. Beim Aufbau eines Elektrolytkondensators geht man zur Erreichung dieses Ziels ganz raffiniert vor. Bild 3.41 zeigt das in vereinfachter Form. Man stellt einfach eine Aluminumblechspirale (als einen der beiden Beläge) in einen Aluminiumzylinder und bringt eine stromleitende, salzhaltige Lösung (Elektrolyt) in das Gefäß. Der Elektrolyt kann in flüssiger, halbflüssiger oder trockener Form eingebracht werden.
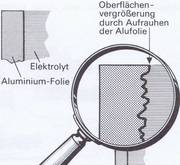
Das Aluminium überzieht sich mit einer hauchdünnen, nichtleitenden Oxidschicht, die so das Dielektrikum bildet (Bild 3.42). Der Abstand der Beläge voneinander ist mithin auf ein äußerstes Mindestmaß reduziert. Aber mehr noch: Um die Oberfläche der sich beeinflussenden Beläge möglichst groß zu machen, rauht man das Aluminiumblech auf. Auf diese Weise ergeben sich die erwähnten hohen Kapazitätswerte auf kleinem Raum. Ein Anschluß (Pluspol) ist mit dem Aluminiumblech verbunden, der zweite wird vom Gehäuse (Minuspol) gebildet, das mit dem Elektrolyten in Kontakt ist.
Auch ein Elektrolytkondensator kann als Wickel hergestellt werden, wenn der Elektrolyt z. B. in halbtrockener Form zwischen die Aluminiumfolie gebracht wird. Eine Prinzipdarstellung zeigt Bild 3.43, wobei Papier als Elektrolytträger dient. Das Ganze ist von einem schützenden Gehäuse umgeben, aus dem die Anschlußenden herausragen (Bild 3.44). Elektrolytkondensatoren dürfen nur an Gleichspannung und nur in der richtigen Polung angeschlossen werden; Plusspannung an den + Pol und Minus an den -Pol des Elektrolytkondensators. Der auf dem Gehäuse aufgedruckte Spannungswert darf nicht überschritten werden.
(1975 !!) Ganz neu: Die Tantal-Kondensatoren
Zu den neueren Entwicklungen auf dem Gebiet der Elektrolyt- kondensatoren gehören die Tantal-Kondensatore. Dieses Material wird anstelle des Aluminiumwickels verwendet, und zwar kann es als Folie, aber auch in gesinterter Form benutzt werden. Das führt zu sehr kleinen Abmessungen. Auch hier ist der Elektrolyt in flüssiger oder trockener Art verwendbar.
Tantal-Kondensatoren haben gute elektrische Eigenschaften und werden - auch wegen ihrer minimalen Größe - vor allem in gedruckten Schaltungen bei niedrigen Betriebsspannungen verwendet. Es gibt sie bereits in Gehäusen mit nur 2-3mm Durchmesser und mit Kapazitätswerten bis 10pF und mehr; die niedrigste Betriebsspannung ist ca. 1.5V.
.
Niedervolt- und Hochvoltausführungen
Elektrolytkondensatoren teilt man in Niedervolt- und Hochvoltausführungen ein. Der Niedervoltbereich reicht bis etwa 100 V, darüber spricht man von Hochvolt Kondensatoren. Letztere gibt es nicht nur in Einfach-, sondern auch in Mehrfachform, wobei sich bis zu vier Kondensatoren in einem Gehäuse befinden (z. B. 200+ 200+75+ 75 up). Bei Niedervolt-Elektrolytkondensatoren liegt die obere Kapazitätsgrenze bei etwa 100000 bis 150000 uF = 100 bis 150 mF.
Die Anschlüsse »Plus« und »Minus« dürfen bei den meisten Elektrolytkondensatoren nicht miteinander vertauscht werden. Eine Ausnahme machen nur bipolare Elektrolytkondcnsatorcn. die beliebig an geschlossen werden können. In den Schaltbildern sind die beiden Arten auf untenstehende Weise gekennzeichnet (Bild 3.45).
Drehkondensatoren
Beim Drehkondensator wird der Kapazitätswert dadurch verändert, daß man ein Plattenpaket (Rotor genannt), das von einem zweiten (dem Stator) isoliert ist, aus diesem heraus- oder in dasselbe hineindreht, so daß einmal größere, einmal kleinere Kapazitätswerte auftreten. Stellen wir uns einen Drehkondensator vor, der nach Bild 3.46 nur aus zwei gegeneinander verdrehbaren Platten besteht (die Platten haben z. B. aus Linearitätsgründen eine besondere Form), so wird sofort deutlich, daß beim Verdrehen eine Änderung der Kapazitätsverhältnisse eintritt. Beim Herausdrehen der beweglichen Platte wird der Kapazitätswert geringer.
Hochwertige Drehkondensatoren haben ein Luftdielektrikum. Die äußeren Platten des Rotors sind geschlitzt, damit man durch leichtes Verbiegen der Sektoren ganz gleichartige Kapazitätsverhältnisse über den gesamten Einstellbereich bei mehreren Kondensatoren mit gemeinsamer Achse schaffen kann (Bild 3.47). Abstimm- Drehkondensatoren in Rundfunkgeräten haben maximale Kapazitätswerte von etwa 500pF (bei hineingedrehtem Plattenpaket) und eine Minimalkapazität von 40—50pF (bei ganz herausgedrehten Platten). Man spricht in diesem Zusammenhang von End- und Anfangskapazität.
Drehkondensatoren mit anderen Dielektrika als Luft (Glimmer, Hartpapier, Kunststoffolie usw.) beanspruchen zwar wesentlich weniger Raum, bringen aber auch Hochfrequenzverluste mit sich. Sie werden deshalb nur dort verwendet, wo ihre kleinen Abmessungen für die Gesamtkonstruktion ausschlaggebend sind, also z. B. in Transistor-Rundfunkgeräten (Bild 3.48).
Trimmer-Kondensatoren
Es gibt noch eine andere Art veränderbarer Kondensatoren, die sogenannten Trimmer. Sie haben kleine Kapazitätswerte und dienen zum »Abgleichen« elektrischer Schwingungskreise, wozu ihr zusätzlicher Kapazitätswert nach dem Abgleichen fest eingestellt bleibt. Trimmer bestehen nach Bild 3.49 z. B. aus runden Keramikscheibchen mit einseitig aufgebrannten Schichten, deren Oberteil drehbar ist.
Philips stellt mit dem in Bild 3.50 gezeigten Lufttrimmer eine sehr verlustarme Ausführung her. Die beiden Kondensatorenflächen werden durch mehrere konzentrisch angeordnete Rohre gebildet, die sich ohne gegenseitiges Berühren ineinanderschieben. Die Kapazität hängt von der Eintauchtiefe ab. Sie wird durch Hineindrehen des Oberteils mittels einer Gewindespindel eingestellt.
Dann gibt es u. a. noch Drahttrimmer. Sie gleichen den Rohrkondensatoren. Ihr Außenbelag besteht jedoch aus einer gelöteten Drahtwicklung (Bild 3.51). Durch teilweises Abwickeln der Windungen lassen sich die gewünschten Kapazitätswerte einstellen, und zwar naturgemäß nur in Richtung auf kleinere Werte.
Stetig verstellbare Drehkondensatoren werden durch einen Pfeil gekennzeichnet. Die nur zum gelegentlichen Einstellen (Abgleichen) bestimmten Trimmer werden so dargestellt wie im rechten Teil von Bild 3.52.
Über die Bezeichnungen und Aufdrucke
Bei den Wickel- und Elektrolytkondensatoren sind die Kapazitätswerte und die Betriebsspannung in Zahlen aufgedruckt.
Bei sehr vielen Kondensatoren werden wie bei den Widerständen sehr häufig Farbringe benutzt. Es gilt dann die gleiche Tabelle wie in Abschnitt 3.1. angegeben. Die Kapazitätstoleranz spielt im allgemeinen nur bei frequenzbestimmenden Kondensatoren (z. B. in Schwingkreisen) eine Rolle. Die üblichen Toleranzen betragen bei normalen Kondensatoren 10 bzw. 20%.
.